1.文章基本信息
期刊:Journal of High Energy Physics (JHEP)
题目:Effective field theories on subspaces of the Bruhat-Tits tree

2.摘要
在Bruhat-Tits树图的两类子空间上分别计算了有效作用量。当子空间被推到树图边界时,这些有效场论退化为了p进数上的同一个共形场论。同时讨论了它们与p进数版本的规范引力对偶的关系。
3.研究动机
3.1小尺度时空的非阿基米德可能性
自然界存在四种基本相互作用:引力,电磁力,强力和弱力。目前我们可以处理后三种相互作用同时存在的情况,或者是仅有引力存在的情况,而无法同时处理四种相互作用。人们相信更好的物理学定律一定会解决这一困难。为了在新物理学定律被找到之前可以一瞥其样貌,人们做了很多尝试来协调引力与其它三种相互作用,比如通过拼凑引力和三种相互作用的部分结论,在某种意义上实现同时研究四种相互作用共存的情况。
如果将引力的基本思想“能量使时空弯曲”与其它三种相互作用里的“不确定关系”结合在一起,人们似乎不得不面对“时空在小尺度上会变得破碎”的结论,如图1。

图1. 小尺度下的时空不再连续(universe-review.ca)
这意味着“继续使用连续的实数来描述小尺度上的时空”这一做法不再恰当。考虑到小尺度时空的破碎结构,有理由猜测我们熟悉的连续时空的某些性质不再成立,比如说“阿基米德性”,即“小的步长可以叠加出大的步长”。于是用“非阿基米德数域”,例如p进数来研究时空的小尺度结构就是合理的了。
由I.V. Volovich提出的“数域不变性原理”还没有被广泛讨论。它听起来应该是正确的,其声称的是“物理学定律应当与观测者所使用的数无关”,即“物理学定律应当在数域的变换下保持不变”。为此,研究其它数域上的物理学就是合理的了。考虑到所有的测量结果都是有理数,于是便有了在包含了有理数的p进数上进行研究的动机。
“规范引力对偶”是一个出自弦论的猜想,它把两个不同维度的理论联系在里一起,可以把某些困难的问题转为为另一维度的简单问题。P进数上的此类研究起步较晚,希望可以作为规范引力对偶的一个重要补充,丰富该研究方向。
Bruhat-Tits树是一张无限大的图,该空间由所有顶点构成,任意两个顶点之间的边的数量反映了两点之间的距离,如图2所示。
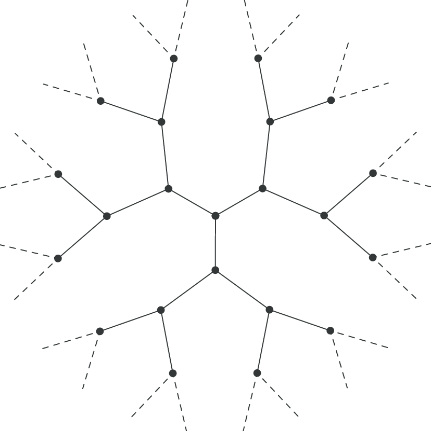
图2. Bruhat-Tits树(Soumya Bhattacharya)
按照规范引力对偶的思想,在整个树图上生活着的场与其边界(是树图的一个子空间,在图2虚线指示的无限远处)上的某个场有着密切的对应关系:将树图上的场在内部(边界以内)的自由度积掉就能得到子空间上的一个场,它是“规范引力对偶”中规范场的“源”。该工作已由前人完成。
4.作者工作
按照规范引力对偶的思想,该子空间不仅可以选择为树图的边界,还可以选择为有限远处的某个,如图3所示。
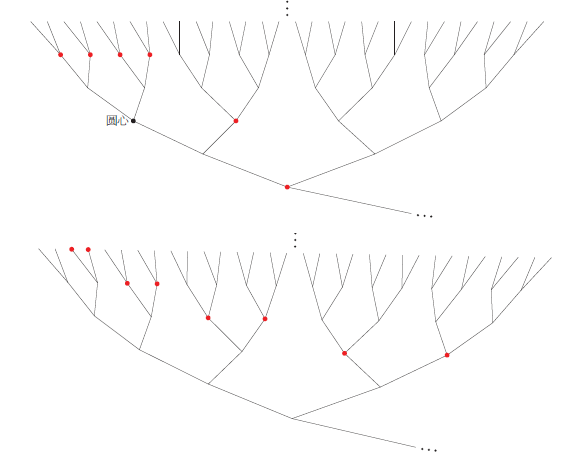
图3. Bruhat-Tits树上的两类子空间(以红色标记):上面的是以某个顶点为圆心的圆;下面的是以某条“直线”为“圆心”的“圆”。
如果将这些子空间推到无限远,即让“圆”的半径趋向于无限大,则它们就退化为整个树图的边界。有研究表明,半径这个参数似乎对应子空间上场论的“能标”,在量子场论中它是十分重要的。
作者在该文章中就完成了这两类子空间上的场论计算,即将树图上的场在子空间以外的自由度全部积掉,得到了对应的有效场论,并做了些规范引力对偶的例行分析(两点函数)。
作者简介
曲峰,毕业于中国科学院理论物理研究所,现从事p进数上的规范引力对偶研究,主要发表文章包括:
Scalar fields on pAdS.
DOI: 10.1016/j.physletb.2018.09.043
The boundary theory of a spinor field theory on the Bruhat-Tits tree.
DOI: 10.1016/j.physletb.2020.135331
Effective field theory on a finite boundary of the Bruhat-Tits tree.
DOI: 10.1103/PhysRevD.103.086015
Effective field theories on subspaces of the Bruhat-Tits tree.
DOI: doi.org/10.1007/JHEP06(2024)175